Limits and Derivatives
Maths NCERT Class 11 Chapter 13
Exercise 13.1 page no: 301
1. Evaluate the Given limit:
Solution:
Given
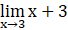
Substituting x = 3, we get
= 3 + 3
= 6
2. Evaluate the Given limit:
Solution:
Given limit: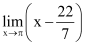
Substituting x = π, we get
= (Ï€ – 22 / 7)
3. Evaluate the Given limit:
Solution:
Given limit:
Substituting r = 1, we get
= π(1)2
= π
4. Evaluate the Given limit:
Solution:
Given limit: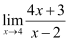
Substituting x = 4, we get
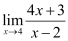= [4(4) + 3] / (4 – 2)
= (16 + 3) / 2
= 19 / 2
5. Evaluate the Given limit:
Solution:
Given limit: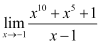
Substituting x = -1, we get
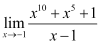
= [(-1)10 + (-1)5 + 1] / (-1 – 1)
= (1 – 1 + 1) / – 2
= – 1 / 2
6. Evaluate the Given limit:
Solution:
Given limit:
= [(0 + 1)5 – 1] / 0
=0
Since, this limit is undefined
Substitute x + 1 = y, then x = y – 1
7. Evaluate the Given limit:
Solution:
8. Evaluate the Given limit:
Solution:
9. Evaluate the Given limit:
Solution:
= [a (0) + b] / c (0) + 1
= b / 1
= b
10. Evaluate the Given limit: 
Solution:
11. Evaluate the Given limit:
Solution:
Given limit:
Substituting x = 1
= [a (1)2 + b (1) + c] / [c (1)2 + b (1) + a]
= (a + b + c) / (a + b + c)
Given
= 1
12. Evaluate the Given limit:
Solution:
By substituting x = – 2, we get
13. Evaluate the Given limit:
Solution:
Given 
14. Evaluate the given limit: 
Solution:
15. Evaluate the given limit:
Solution:
16. Evaluate the given limit:
Solution:
17. Evaluate the given limit:
Solution:
18. Evaluate the given limit:
Solution:
19. Evaluate the given limit:
Solution:
20. Evaluate the given limit:
Solution:
21. Evaluate the given limit:
Solution:
22. Evaluate the given limit:
Solution:
23.
Solution:
24. Find
, where
Solution:
25. Evaluate
, where f(x) =
Solution:
26. Find
, where f (x) =
Solution:
27. Find
, where
Solution:
28. Suppose
and if
what are possible values of a and b
Solution:
29. Let a1, a2,………an be fixed real numbers and define a function
f (x) = (x – a1) (x – a2) ……. (x – an).
What is
For some a ≠ a1, a2, ……. an, compute
Solution:
30. If 
For what value (s) of a does 
exists?
Solution:
31. If the function f(x) satisfies 
, evaluate
Solution:
32. If 
For what integers m and n does both 
and 
exist?
Solution:
Exercise 13.2 page no: 312
1. Find the derivative of x2– 2 at x = 10
Solution:
Let f (x) = x2 – 2
From first principle
2. Find the derivative of x at x = 1.
Solution:
Let f (x) = x
Then,
3. Find the derivative of 99x at x = l00.
Solution:
Let f (x) = 99x,
From first principle
= 99
4. Find the derivative of the following functions from first principle
(i) x3 – 27
(ii) (x – 1) (x – 2)
(iii) 1 / x2
(iv) x + 1 / x – 1
Solution:
(i) Let f (x) = x3 – 27
From first principle
(ii) Let f (x) = (x – 1) (x – 2)
From first principle
(iii) Let f (x) = 1 / x2
From first principle, we get
(iv) Let f (x) = x + 1 / x – 1
From first principle, we get
5. For the function 
.Prove that f’ (1) =100 f’ (0).
Solution:
6. Find the derivative of 
for some fixed real number a.
Solution:
7. For some constants a and b, find the derivative of
(i) (x − a) (x − b)
(ii) (ax2 + b)2
(iii) x – a / x – b
Solution:
(i) (x – a) (x – b)
(ii) (ax2 + b)2
= 4ax(ax2 + b)
(iii) x – a / x – b
8. Find the derivative of 
for some constant a.
Solution:
9. Find the derivative of
(i) 2x – 3 / 4
(ii) (5x3 + 3x – 1) (x – 1)
(iii) x-3 (5 + 3x)
(iv) x5 (3 – 6x-9)
(v) x-4 (3 – 4x-5)
(vi) (2 / x + 1) – x2 / 3x – 1
Solution:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
10. Find the derivative of cos x from first principle
Solution:
11. Find the derivative of the following functions:
(i) sin x cos x
(ii) sec x
(iii) 5 sec x + 4 cos x
(iv) cosec x
(v) 3 cot x + 5 cosec x
(vi) 5 sin x – 6 cos x + 7
(vii) 2 tan x – 7 sec x
Solution:
(i) sin x cos x
(ii) sec x
(iii) 5 sec x + 4 cos x
(iv) cosec x
(v) 3 cot x + 5 cosec x
(vi)5 sin x – 6 cos x + 7
(vii) 2 tan x – 7 sec x
Miscellaneous exercise page no: 317
1. Find the derivative of the following functions from first principle:
(i) –x
(ii) (–x)–1
(iii) sin (x + 1)
(iv) 
Solution:
(ii) (-x)-1
= 1 / x2
(iii) sin (x + 1)
(iv) 
We get,
Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
2. (x + a)
Solution:
3. (px + q) (r / x + s)
Solution:
4. (ax + b) (cx + d)2
Solution:
5. (ax + b) / (cx + d)
Solution:
6. (1 + 1 / x) / (1 – 1 / x)
Solution:
7. 1 / (ax2 + bx + c)
Solution:
8. (ax + b) / px2 + qx + r
Solution:
9. (px2 + qx + r) / ax + b
Solution:
10. (a / x4) – (b / x2) + cox x
Solution:
11. 
Solution:
12. (ax + b)n
Solution:
13. (ax + b)n (cx + d)m
Solution:
14. sin (x + a)
Solution:
15. cosec x cot x
Solution:
So, we get
16. 
Solution:
17.
Solution:
18.
Solution:
19. sinn x
Solution:
20. 
Solution:
21.
Solution:
22. x4 (5 sin x – 3 cos x)
Solution:
23. (x2 + 1) cos x
Solution:
24. (ax2 + sin x) (p + q cos x)
Solution:
25. 
Solution:
26. 
Solution:
27. 
Solution:
28. 
Solution:
29. (x + sec x) (x – tan x)
Solution:
30. 
Solution:
0 Comments